Prüfröhrchen nach KARSTEN: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 5: | Zeile 5: | ||
zurück zu [[Wasseraufnahmekoeffizient]] <br> | zurück zu [[Wasseraufnahmekoeffizient]] <br> | ||
== Einleitung == | |||
Eine Zusammenfassung des Artikels ''“Bestimmung der kapillaren Wasseraufnahme mit Messröhrchen nach Karsten und Mirowski“ aus dem im IRB-Verlag 2011 erschienen Buch “Leitfaden Naturstein-Monitoring''“ <ref>http://www.baufachinformation.de/buch/234648 http://www.baufachinformation.de/buch/234648]; letzter Zugriff am 8.5.2013</ref> hinsichtlich der Messmethode zur Abschätzung des w-Wertes mit dem Karsten`schen Prüfröhrchen ergänzt um den mathematischen Hintergrund des Auswerteverfahrens. | Eine Zusammenfassung des Artikels ''“Bestimmung der kapillaren Wasseraufnahme mit Messröhrchen nach Karsten und Mirowski“ aus dem im IRB-Verlag 2011 erschienen Buch “Leitfaden Naturstein-Monitoring''“ <ref>http://www.baufachinformation.de/buch/234648 http://www.baufachinformation.de/buch/234648]; letzter Zugriff am 8.5.2013</ref> hinsichtlich der Messmethode zur Abschätzung des w-Wertes mit dem Karsten`schen Prüfröhrchen ergänzt um den mathematischen Hintergrund des Auswerteverfahrens. | ||
| Zeile 13: | Zeile 15: | ||
== Durchführung der Messung mit dem Karsten`schen Prüfröhrchen == | |||
Das Prüfröhrchen nach Karsten besteht aus einem nach einer Seite offenem und mit einem flachen Rand versehenen Glaszylinder (Glocke), der an der Objektoberfläche aufgekittet wird, und einem gradierten Rohr, an dessen Skala im Verlauf der Messung die aufgenommene Flüssigkeitsmenge abgelesen wird. (s. Abb. 1). Zum Befestigen des Glasröhrchens am Untergrund können geeignete Kittmassen verwendet werden. Der geschmeidig geknetete Kitt wird zu einem dünnen Wulst ausgerollt und auf dem Glasrand des Karstenröhrchens angedrückt (s. Abb. 2), und dann der runde Glaskörper fest an die Wandoberfläche appliziert. Wulstüberstände sollten mit einem kleinen Spatel glasbündig abgeschnitten werden, sofern die Untergrundanhaftung dies zulässt. Hierbei sollte das Karstenglas gut an die Wand gedrückt werden. Der bündige Abschluss des Kittes mit dem Glasrand ermöglicht das frühzeitige Wahrnehmen eines Durchfeuchtungshofes um das Messröhrchen. | Das Prüfröhrchen nach Karsten besteht aus einem nach einer Seite offenem und mit einem flachen Rand versehenen Glaszylinder (Glocke), der an der Objektoberfläche aufgekittet wird, und einem gradierten Rohr, an dessen Skala im Verlauf der Messung die aufgenommene Flüssigkeitsmenge abgelesen wird. (s. Abb. 1). Zum Befestigen des Glasröhrchens am Untergrund können geeignete Kittmassen verwendet werden. Der geschmeidig geknetete Kitt wird zu einem dünnen Wulst ausgerollt und auf dem Glasrand des Karstenröhrchens angedrückt (s. Abb. 2), und dann der runde Glaskörper fest an die Wandoberfläche appliziert. Wulstüberstände sollten mit einem kleinen Spatel glasbündig abgeschnitten werden, sofern die Untergrundanhaftung dies zulässt. Hierbei sollte das Karstenglas gut an die Wand gedrückt werden. Der bündige Abschluss des Kittes mit dem Glasrand ermöglicht das frühzeitige Wahrnehmen eines Durchfeuchtungshofes um das Messröhrchen. | ||
| Zeile 33: | Zeile 33: | ||
<br clear="all"> | <br clear="all"> | ||
== Auswertung der Messdaten == | |||
Bei dieser Auswertung wird der w-Wert nicht rein mathematisch berechnet, sondern durch Vergleich der Messwertkurve mit einer rechnerisch generierten Kurvenschar visuell abgeschätzt. Die Kurvenschar basiert auf der Angabe der wirksamen Saugfläche, eines möglichst realitätsnahen Wertes für die Wasseraufnahmekapazität und auf einem frei wählbaren Intervall für den w-Wert. Durch Variieren des w-Wert-Intervalls wird versucht, die Kurvenschar bzw. eine dieser Kurven der Messwertkurve so anzunähern, dass sie im Idealfall diese überlagert oder ihr sehr ähnlich wird. Je genauer die Übereinstimmung ist, desto wahrscheinlicher entspricht der w-Wert, der der rechnerischen Kurve zu Grunde liegt, dem des Baustoffes. | Bei dieser Auswertung wird der w-Wert nicht rein mathematisch berechnet, sondern durch Vergleich der Messwertkurve mit einer rechnerisch generierten Kurvenschar visuell abgeschätzt. Die Kurvenschar basiert auf der Angabe der wirksamen Saugfläche, eines möglichst realitätsnahen Wertes für die Wasseraufnahmekapazität und auf einem frei wählbaren Intervall für den w-Wert. Durch Variieren des w-Wert-Intervalls wird versucht, die Kurvenschar bzw. eine dieser Kurven der Messwertkurve so anzunähern, dass sie im Idealfall diese überlagert oder ihr sehr ähnlich wird. Je genauer die Übereinstimmung ist, desto wahrscheinlicher entspricht der w-Wert, der der rechnerischen Kurve zu Grunde liegt, dem des Baustoffes. | ||
Das Programm umfasst vier türkis unterlegte Blöcke in denen Daten eingegeben werden; die Eingabefelder sind rot umrandet (siehe Abb. 3). Bei „Allgemeine Angaben“ sind Objektdaten einzutragen. In die Tabelle „Messwerteingabe“ wird das aufgenommene Wasservolumen [ml] und die entsprechenden Eindringzeiten [min, sec] eingetragen (bis zu 15 Messwertpaare); bei der Zeit ist darauf zu achten, dass die Minuten von den Sekunden durch ein Komma getrennt sind (!). Sobald hier Messwerte eingetragen werden, erscheint im Diagramm neben der Tabelle die Messwertkurve (rot). In dem Block „Dateneingabe“ werden Werte für den Durchmesser des Karsten`schen Prüfröhrchen, für die Wasseraufnahmekapazität (WAK) und für den zu erwartenden w-Wert Bereich eingegeben. Der einzutragende material- und zustandsspezifische WAK-Wert sollte möglichst realistisch sein (auf der Basis eigener Messungen an Objektproben oder von Literaturdaten). Im Diagramm darunter erscheint nun eine Kurvenschar bestehend aus fünf (farbigen) Kurven. Durch das Variieren der Vorgabebereiche für den w-Wert kann eine dieser Kurven der Messwertkurve angeglichen werden. Der w-Wert für diese Kurve ist aus der Legende im Diagramm zu ersehen; bei hinreichender Annäherung kann so der w-Wert für die Messung bestimmtwerden. Es ist allerdings darauf zu achten,dass die Daten in diesem Block einen Realitätsbezug haben; z.B. bei einer WAK > 30 Vol.-% erscheint die Frage: “Ist der Wert für WAK realistisch?“. Der aus dem Diagramm ermittelte w-Wert wird in die Tabelle (4. Block) „Ergebnisse“ eingetragen. Es erscheint außer dem eingegebenen WAK und dem daraus ermittelten w-Wert auch das aus diesen beiden Angaben errechnete Ergebnis für den Wassereindringkoeffizienten (B-Wert). | |||
dass die Daten in diesem Block einen Realitätsbezug haben; z.B. bei einer WAK > 30 Vol.-% erscheint die Frage: “Ist der Wert für WAK realistisch?“. Der aus dem Diagramm ermittelte w-Wert wird in die Tabelle (4. Block) „Ergebnisse“ eingetragen. Es erscheint außer dem eingegebenen WAK und dem daraus ermittelten w-Wert auch das aus diesen beiden Angaben errechnete Ergebnis für den Wassereindringkoeffizienten (B-Wert). | |||
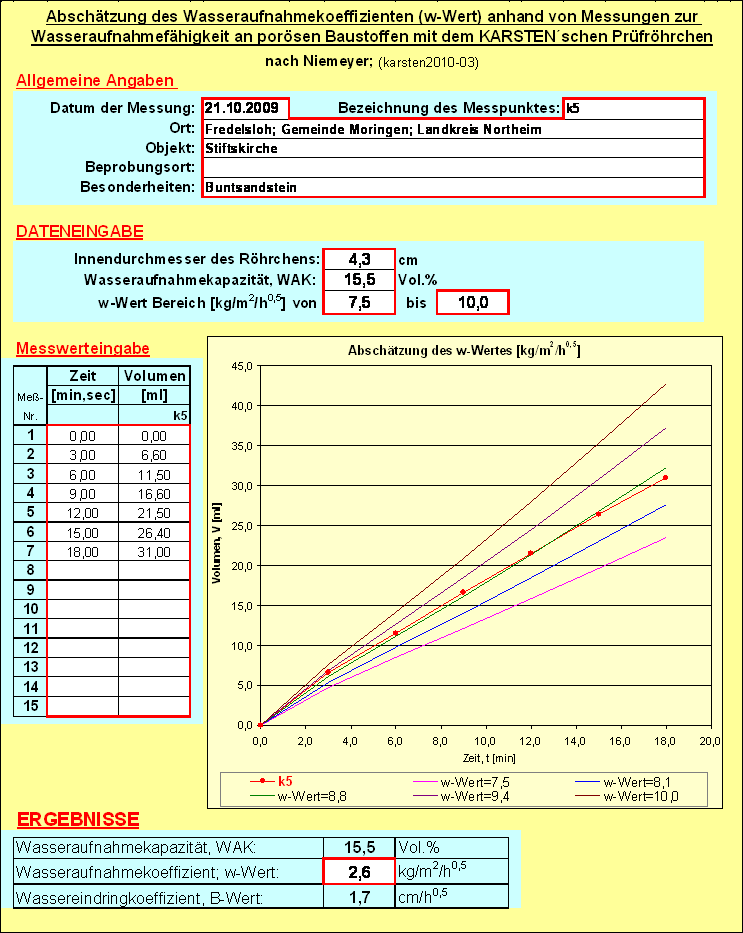
[[File:Karsten 3.png|right|392px|Abb.3: Maske zur Auswertung der kapillaren Wasseraufnahme nach Karsten]] | |||
Die obige Auswertemaske entstammt der gleichnamigen Excel-Datei, “karsten2010-03“ | Die obige Auswertemaske entstammt der gleichnamigen Excel-Datei, “karsten2010-03“ | ||
== Mathematische Erläuterungen zur Auswertung der Messdaten == | |||
In dem Diagramm des obigen Auswerteschemas ist der w-Wert (w) eine Funktion des zeitabhängig kapillar aufgenommenen Wassers; diese Wassermenge (V) wird in Milliliter am Röhrchen abgelesen. | In dem Diagramm des obigen Auswerteschemas ist der w-Wert (w) eine Funktion des zeitabhängig kapillar aufgenommenen Wassers; diese Wassermenge (V) wird in Milliliter am Röhrchen abgelesen. | ||
| Zeile 83: | Zeile 67: | ||
=== Kapillare Wasseraufnahme === | |||
Im Labor werden üblicherweise die Wasseraufnahmekoeffizienten (w-Werte) von Baustoffen durch kapillare Wasseraufnahme an Bohrkernen oder Prismen bestimmt. Die Wasseraufnahme erfolgt über einen Saugvorgang in eindimensionaler Richtung. Dabei ist in erster Näherung die aufgenommene Wassermenge (m) proportional der Wurzel aus der Zeit (t).und ist von der Größe der Saugfläche (A) abhängig. Es gilt folgende Gleichung: | Im Labor werden üblicherweise die Wasseraufnahmekoeffizienten (w-Werte) von Baustoffen durch kapillare Wasseraufnahme an Bohrkernen oder Prismen bestimmt. Die Wasseraufnahme erfolgt über einen Saugvorgang in eindimensionaler Richtung. Dabei ist in erster Näherung die aufgenommene Wassermenge (m) proportional der Wurzel aus der Zeit (t).und ist von der Größe der Saugfläche (A) abhängig. Es gilt folgende Gleichung: | ||
Gl.(1): <math>w=\frac{m}{A\cdot\sqrt{t}}\\</math> | Gl.(1): <math>w=\frac{m}{A\cdot\sqrt{t}}\\</math> | ||
w wird als Wasseraufnahmekoeffizient (w-Wert) bezeichnet und in kg/m<sup>2</sup>/h<sup>0,5</sup> angegeben. | w wird als Wasseraufnahmekoeffizient (w-Wert) bezeichnet und in kg/m<sup>2</sup>/h<sup>0,5</sup> angegeben. | ||
Ebenso kann ein Wassereindringkoeffizient (B-Wert) definiert werden. Dabei gilt näherungsweise, dass die Wassereindringtiefe (x) proportional der Wurzel aus der Zeit (t) ist. | Ebenso kann ein Wassereindringkoeffizient (B-Wert) definiert werden. Dabei gilt näherungsweise, dass die Wassereindringtiefe (x) proportional der Wurzel aus der Zeit (t) ist. | ||
Gl.(2): <math>B=\frac{x}{\sqrt{t}}\\</math> | Gl.(2): <math>B=\frac{x}{\sqrt{t}}\\</math> | ||
Aus dem w- und B-Wert wird die Wasseraufnahmekapazität (WAK) unter Berücksichtigung von | Aus dem w- und B-Wert wird die Wasseraufnahmekapazität (WAK) unter Berücksichtigung von | ||
Gl.(3) <math>\delta=\frac{m}{V}\\</math> | Gl.(3) <math>\delta=\frac{m}{V}\\</math> | ||
wie folgt hergeleitet: | wie folgt hergeleitet: | ||
Gl.(4): <math>WAK=\frac{w}{B\cdot\delta}\\</math> | Gl.(4): <math>WAK=\frac{w}{B\cdot\delta}\\</math> | ||
| Zeile 128: | Zeile 101: | ||
Die Wasseraufnahmekapazität (WAK) wird häufig auch in Volumenprozent angegeben: | Die Wasseraufnahmekapazität (WAK) wird häufig auch in Volumenprozent angegeben: | ||
Gl.(5)''' <math>WAK\left[Vol.\%\right]=WAK\cdot 100\\</math> | Gl.(5)''' <math>WAK\left[Vol.\%\right]=WAK\cdot 100\\</math> | ||
Durch einsetzen von Gleichung 2 in Gleichung 4 ergibt sich für die Eindringtiefe (x): | Durch einsetzen von Gleichung 2 in Gleichung 4 ergibt sich für die Eindringtiefe (x): | ||
| Zeile 142: | Zeile 112: | ||
===Wasseraufnahme nach Karsten=== | |||
| Zeile 152: | Zeile 120: | ||
Im Idealfall besitzt der Durchfeuchtungskörper die Form eines zentralen Zylinders, der von einem Vierteltorus umgeben ist. Die Grundfläche des Zylinders entspricht der des Karsten`schen Prüfröhrchens. | Im Idealfall besitzt der Durchfeuchtungskörper die Form eines zentralen Zylinders, der von einem Vierteltorus umgeben ist. Die Grundfläche des Zylinders entspricht der des Karsten`schen Prüfröhrchens. | ||
Gl.(7): <math>V_{Zylinder}=\pi\cdot r^2\cdot x\\</math> | Gl.(7): <math>V_{Zylinder}=\pi\cdot r^2\cdot x\\</math> | ||
| Zeile 166: | Zeile 132: | ||
<u>3.2.1.) Guldinsche Regel:</u> | <u>3.2.1.) Guldinsche Regel:</u> | ||
Das Volumen des Vierteltorus lässt sich mit der Guldinschen Regel berechnen. Diese besagt: | Das Volumen des Vierteltorus lässt sich mit der Guldinschen Regel berechnen. Diese besagt: | ||
Das Volumen eines Drehkörpers ist gleich dem Produkt aus dem Flächeninhalt der den Drehkörper erzeugende Fläche und der Länge des Weges, den der Schwerpunkt dieser Fläche bei einer Volldrehung um die Drehachse beschreibt. | Das Volumen eines Drehkörpers ist gleich dem Produkt aus dem Flächeninhalt der den Drehkörper erzeugende Fläche und der Länge des Weges, den der Schwerpunkt dieser Fläche bei einer Volldrehung um die Drehachse beschreibt. | ||
| Zeile 176: | Zeile 140: | ||
===Berechnung des Vierteltorus=== | |||
Um nun das Volumen des Vierteltorus nach dieser Regel berechnen zu können, benötigt man den Abstand zwischen der Drehachse und dem Schwerpunkt des Viertelkreises. Dieser Viertelkreis erzeugt durch eine Volldrehung seines Schwerpunktes um die Drehachse einen Vierteltorus. Genauso kann ein Halbkreis einen Vierteltorus erzeugen, wenn der sich ergebene Drehkörper senkrecht zur Drehachse halbiert wird. | Um nun das Volumen des Vierteltorus nach dieser Regel berechnen zu können, benötigt man den Abstand zwischen der Drehachse und dem Schwerpunkt des Viertelkreises. Dieser Viertelkreis erzeugt durch eine Volldrehung seines Schwerpunktes um die Drehachse einen Vierteltorus. Genauso kann ein Halbkreis einen Vierteltorus erzeugen, wenn der sich ergebene Drehkörper senkrecht zur Drehachse halbiert wird. | ||
| Zeile 187: | Zeile 150: | ||
Gl.(8): <math>V_{Kugel}=\frac{4\cdot\pi \cdot x^3}{3}\\</math> | Gl.(8): <math>V_{Kugel}=\frac{4\cdot\pi \cdot x^3}{3}\\</math> | ||
x = Radius der Kugel; (entspricht in dieser Berechnung der Wassereindringtiefe) | x = Radius der Kugel; (entspricht in dieser Berechnung der Wassereindringtiefe) | ||
Mittels der Guldinschen Regel wird nun der Abstand (a) von der Drehachse bis zum Schwerpunkt des Halbkreises berechnet. | Mittels der Guldinschen Regel wird nun der Abstand (a) von der Drehachse bis zum Schwerpunkt des Halbkreises berechnet. | ||
Gl.(9): <math>\frac{4\cdot\pi \cdot x^3}{3}=\left(\frac{\pi\cdot x^2}{2}\right)\cdot (2\cdot\pi\cdot a)\\</math> | Gl.(9): <math>\frac{4\cdot\pi \cdot x^3}{3}=\left(\frac{\pi\cdot x^2}{2}\right)\cdot (2\cdot\pi\cdot a)\\</math> | ||
V<sub>Kugel</sub> = (Fläche des Halbkreises) '''<sup>.</sup>''' (Weg des Schwerpunktes um die Drehachse) | V<sub>Kugel</sub> = (Fläche des Halbkreises) '''<sup>.</sup>''' (Weg des Schwerpunktes um die Drehachse) | ||
| Zeile 207: | Zeile 165: | ||
Auflösen nach a: | Auflösen nach a: | ||
Gl.(10): <math>a=\frac{4\cdot x}{3\cdot \pi}\\</math> | Gl.(10): <math>a=\frac{4\cdot x}{3\cdot \pi}\\</math> | ||
a = Entfernung des Schwerpunktes von der Drehachse | a = Entfernung des Schwerpunktes von der Drehachse | ||
Der Schwerpunkt des Halbkreises ist von dessen Entfernung zur Drehachse unabhängig. | Der Schwerpunkt des Halbkreises ist von dessen Entfernung zur Drehachse unabhängig. | ||
Wird diese Entfernung (a) um den Radius (r) des Karsten´schen Prüfröhrchens verlängert und der sich ausbildende Drehkörper senkrecht zur Drehachse halbiert, so erhält man das Volumen des Vierteltorus. a wird wie laut Gleichung 10 ersetzt. | Wird diese Entfernung (a) um den Radius (r) des Karsten´schen Prüfröhrchens verlängert und der sich ausbildende Drehkörper senkrecht zur Drehachse halbiert, so erhält man das Volumen des Vierteltorus. a wird wie laut Gleichung 10 ersetzt. | ||
Gl.(11) <math>_{VT}=\frac{\left(\frac{\pi\cdot x^2}{2}\right)\cdot (2\cdot\pi\cdot (r+a))}{2}=\frac{\pi^2\cdot r \cdot x^2}{2}+\frac{2\cdot \pi \cdot x^3}{3}\\</math> | Gl.(11) <math>_{VT}=\frac{\left(\frac{\pi\cdot x^2}{2}\right)\cdot (2\cdot\pi\cdot (r+a))}{2}=\frac{\pi^2\cdot r \cdot x^2}{2}+\frac{2\cdot \pi \cdot x^3}{3}\\</math> | ||
| Zeile 233: | Zeile 185: | ||
<br clear="all"> | <br clear="all"> | ||
===Berechnung des Durchdringungskörper=== | |||
Wird jetzt zum Volumen des Vierteltorus(Gl.10) noch das Volumen des zentralen Zylinders (Gl.7) addiert, erhält man das gesamte Durchfeuchtungsvolumen (V<sub>Dkar</sub>), welches sich bei der Wasseraufnahme mit dem Karsten`schen Prüfröhrchen ausbildet: | Wird jetzt zum Volumen des Vierteltorus(Gl.10) noch das Volumen des zentralen Zylinders (Gl.7) addiert, erhält man das gesamte Durchfeuchtungsvolumen (V<sub>Dkar</sub>), welches sich bei der Wasseraufnahme mit dem Karsten`schen Prüfröhrchen ausbildet: | ||
| Zeile 244: | Zeile 194: | ||
<u>3.3.) Berechnung des zeitabhängig kapillar aufgenommenen Wassers bei der Messmethode mit dem Karsten`schen Prüfröhrchen:</u> | <u>3.3.) Berechnung des zeitabhängig kapillar aufgenommenen Wassers bei der Messmethode mit dem Karsten`schen Prüfröhrchen:</u> | ||
Die Wasseraufnahme wie auch die Wasseraufnahmekapazität eines Gesteins ist unabhängig von dessen Gewicht und dessen Volumen und somit auch von seiner Form. Dies bedeutet, dass das Verhältnis der Volumina der jeweils aufgenommenen Wassermenge zu deren Durchfeuchtungsvolumina in einem Körper bzw. einem Stein immer konstant bleibt. Daraus folgt: | Die Wasseraufnahme wie auch die Wasseraufnahmekapazität eines Gesteins ist unabhängig von dessen Gewicht und dessen Volumen und somit auch von seiner Form. Dies bedeutet, dass das Verhältnis der Volumina der jeweils aufgenommenen Wassermenge zu deren Durchfeuchtungsvolumina in einem Körper bzw. einem Stein immer konstant bleibt. Daraus folgt: | ||
Gl.(13): <math>\frac{V_{kap}}{V_{Dkap}}=\frac{V_{kar}}{V_{Dkar}}\\</math> | Gl.(13): <math>\frac{V_{kap}}{V_{Dkap}}=\frac{V_{kar}}{V_{Dkar}}\\</math> | ||
V<sub>kap</sub> : Aufgenommenes Wasservolumen bei kapillarer Wasseraufnahme mit eindimensionaler Saugrichtung | V<sub>kap</sub> : Aufgenommenes Wasservolumen bei kapillarer Wasseraufnahme mit eindimensionaler Saugrichtung | ||
V<sub>Dkap </sub>: Durchfeuchtungsvolumen bei kapillarer Wasseraufnahme mit eindimensionaler Saugrichtung | V<sub>Dkap </sub>: Durchfeuchtungsvolumen bei kapillarer Wasseraufnahme mit eindimensionaler Saugrichtung | ||
V<sub>kar</sub> : Aufgenommenes Wasservolumen bei Wasseraufnahme nach Karsten (dreidimensionale Saugrichtung) | V<sub>kar</sub> : Aufgenommenes Wasservolumen bei Wasseraufnahme nach Karsten (dreidimensionale Saugrichtung) | ||
V<sub>Dkar</sub> : Durchfeuchtungsvolumen bei Wasseraufnahme nach Karsten (dreidimensionale Saugrichtung) | V<sub>Dkar</sub> : Durchfeuchtungsvolumen bei Wasseraufnahme nach Karsten (dreidimensionale Saugrichtung) | ||
====Berechnung von V<sub>kap</sub>==== | |||
| Zeile 280: | Zeile 220: | ||
====Berechnung von V<sub>Dkap</sub>==== | |||
Gl.(16): <math>V_{Dkap}=A\cdot x\\</math> | Gl.(16): <math>V_{Dkap}=A\cdot x\\</math> | ||
A = Grundfläche des Karsten`schen Prüfröhrchens (zentraler Zylinder) | A = Grundfläche des Karsten`schen Prüfröhrchens (zentraler Zylinder) | ||
x = Wassereindringtiefe | x = Wassereindringtiefe | ||
| Zeile 317: | Zeile 249: | ||
Gl.(19): <math>V_{kar}=WAK\cdot \pi\cdot r^2\cdot x+\frac{WAK\cdot\pi^2\cdot r\cdot x^2}{2}+\frac{2\cdot WAK\cdot \pi\cdot x^3}{3}\\</math> | Gl.(19): <math>V_{kar}=WAK\cdot \pi\cdot r^2\cdot x+\frac{WAK\cdot\pi^2\cdot r\cdot x^2}{2}+\frac{2\cdot WAK\cdot \pi\cdot x^3}{3}\\</math> | ||
Bei der Auswertung wird nicht der Radius (r) des Karsten`schen Röhrchens angegeben, sondern der Durchmesser (s.a. Gleichung 20) | Bei der Auswertung wird nicht der Radius (r) des Karsten`schen Röhrchens angegeben, sondern der Durchmesser (s.a. Gleichung 20) | ||
| Zeile 327: | Zeile 257: | ||
Gl.(20): <math>V_{kar}=\frac{\pi\cdot d^2\cdot w\cdot\sqrt{t}}{4\cdot \delta}+\frac{\pi^2\cdot d\cdot w^2\cdot t}{4\cdot WAK\cdot \delta^2}+\frac{2\cdot\pi\cdot w^3\cdot t\cdot\sqrt{t}}{3\cdot WAK^2\cdot \delta^3}\\</math> | Gl.(20): <math>V_{kar}=\frac{\pi\cdot d^2\cdot w\cdot\sqrt{t}}{4\cdot \delta}+\frac{\pi^2\cdot d\cdot w^2\cdot t}{4\cdot WAK\cdot \delta^2}+\frac{2\cdot\pi\cdot w^3\cdot t\cdot\sqrt{t}}{3\cdot WAK^2\cdot \delta^3}\\</math> | ||
Werden die entsprechenden Parameter in diese Formel wie folgt eingetragen: | Werden die entsprechenden Parameter in diese Formel wie folgt eingetragen: | ||
Version vom 24. September 2013, 15:02 Uhr
Bestimmung der kapillaren Wasseraufnahme mit dem Prüfröhrchen nach Karsten
Autor: Rolf Niemeyer
zurück zu Wasseraufnahmekoeffizient
Einleitung[Bearbeiten]
Eine Zusammenfassung des Artikels “Bestimmung der kapillaren Wasseraufnahme mit Messröhrchen nach Karsten und Mirowski“ aus dem im IRB-Verlag 2011 erschienen Buch “Leitfaden Naturstein-Monitoring“ [1] hinsichtlich der Messmethode zur Abschätzung des w-Wertes mit dem Karsten`schen Prüfröhrchen ergänzt um den mathematischen Hintergrund des Auswerteverfahrens.
Die Kenntnis der kapillaren Wasseraufnahme ist für die Zustandsbeurteilung vieler Monitoringobjekte von großem Interesse, z. B. zur Wirksamkeitsüberprüfung einer Hydrophobierung, zur Einschätzung der Notwendigkeit und Wirksamkeit von Reinigungsmaßnahmen oder zur Beurteilung von Fugenmörteln, Ersatzmörteln und Schlämmen. Einschlägige Kenngrößen sind der Wasseraufnahmekoeffizient w [kg/(m²√h)], der Wassereindringkoeffizient B [cm/√h] und die Wasseraufnahmekapazität WAK [Vol.-%], die mathematisch miteinander verknüpft sind. Sie lassen sich mit Exaktheit nur durch Labormessungen an Objektproben definierter Geometrie nach einschlägigen Normen bestimmen. Allerdings sind zerstörende Beprobungen wie z. B. Bohrkernentnahmen an Denkmalobjekten vielfach nicht akzeptabel. Am Objekt können allerdings mit dem Prüfröhrchen nach Karsten die Kenngrößen der kapillaren Wasseraufnahme zerstörungsfrei abgeschätzt werden.
Durchführung der Messung mit dem Karsten`schen Prüfröhrchen[Bearbeiten]
Das Prüfröhrchen nach Karsten besteht aus einem nach einer Seite offenem und mit einem flachen Rand versehenen Glaszylinder (Glocke), der an der Objektoberfläche aufgekittet wird, und einem gradierten Rohr, an dessen Skala im Verlauf der Messung die aufgenommene Flüssigkeitsmenge abgelesen wird. (s. Abb. 1). Zum Befestigen des Glasröhrchens am Untergrund können geeignete Kittmassen verwendet werden. Der geschmeidig geknetete Kitt wird zu einem dünnen Wulst ausgerollt und auf dem Glasrand des Karstenröhrchens angedrückt (s. Abb. 2), und dann der runde Glaskörper fest an die Wandoberfläche appliziert. Wulstüberstände sollten mit einem kleinen Spatel glasbündig abgeschnitten werden, sofern die Untergrundanhaftung dies zulässt. Hierbei sollte das Karstenglas gut an die Wand gedrückt werden. Der bündige Abschluss des Kittes mit dem Glasrand ermöglicht das frühzeitige Wahrnehmen eines Durchfeuchtungshofes um das Messröhrchen.

|
" " | 
|
| Abb. 1: Karstenröhrchen | Abb. 2: Kittwulst vor dem Andrücken des Röhrchens |
Nach dem Aufkitten wird die Vorrichtung über das gradierte Messrohr zügig mit einer Spritzflasche bis zur Linie von 0 ml mit entmineralisiertem Wasser befüllt und gleichzeitig die Zeitmessung gestartet. Nachfolgend werden in beliebigen Zeitabständen die aufgenommenen Wassermengen und die dazugehörigen Eindringzeiten dokumentiert; empfehlenswert sind häufigere Ablesungen zu Messbeginn. Sobald Leckagen wie zum Beispiel Auslaufen des Röhrchens auftreten wird die Messung abgebrochen. Zur Verbesserung der Messgenauigkeit empfiehlt es sich nach Abschluss der Messung das Röhrchen vorsichtig abzunehmen um den Durchmesser des Kittwulstes messen zu können. Denn die zeitabhängig aufgenommene Wassermenge wird nicht vom Nenndurchmesser der Glasglocke sondern von der jeweiligen Ausformung des Kittwulstes und somit von der tatsächlichen Saugfläche beeinflusst.
Auswertung der Messdaten[Bearbeiten]
Bei dieser Auswertung wird der w-Wert nicht rein mathematisch berechnet, sondern durch Vergleich der Messwertkurve mit einer rechnerisch generierten Kurvenschar visuell abgeschätzt. Die Kurvenschar basiert auf der Angabe der wirksamen Saugfläche, eines möglichst realitätsnahen Wertes für die Wasseraufnahmekapazität und auf einem frei wählbaren Intervall für den w-Wert. Durch Variieren des w-Wert-Intervalls wird versucht, die Kurvenschar bzw. eine dieser Kurven der Messwertkurve so anzunähern, dass sie im Idealfall diese überlagert oder ihr sehr ähnlich wird. Je genauer die Übereinstimmung ist, desto wahrscheinlicher entspricht der w-Wert, der der rechnerischen Kurve zu Grunde liegt, dem des Baustoffes.
Das Programm umfasst vier türkis unterlegte Blöcke in denen Daten eingegeben werden; die Eingabefelder sind rot umrandet (siehe Abb. 3). Bei „Allgemeine Angaben“ sind Objektdaten einzutragen. In die Tabelle „Messwerteingabe“ wird das aufgenommene Wasservolumen [ml] und die entsprechenden Eindringzeiten [min, sec] eingetragen (bis zu 15 Messwertpaare); bei der Zeit ist darauf zu achten, dass die Minuten von den Sekunden durch ein Komma getrennt sind (!). Sobald hier Messwerte eingetragen werden, erscheint im Diagramm neben der Tabelle die Messwertkurve (rot). In dem Block „Dateneingabe“ werden Werte für den Durchmesser des Karsten`schen Prüfröhrchen, für die Wasseraufnahmekapazität (WAK) und für den zu erwartenden w-Wert Bereich eingegeben. Der einzutragende material- und zustandsspezifische WAK-Wert sollte möglichst realistisch sein (auf der Basis eigener Messungen an Objektproben oder von Literaturdaten). Im Diagramm darunter erscheint nun eine Kurvenschar bestehend aus fünf (farbigen) Kurven. Durch das Variieren der Vorgabebereiche für den w-Wert kann eine dieser Kurven der Messwertkurve angeglichen werden. Der w-Wert für diese Kurve ist aus der Legende im Diagramm zu ersehen; bei hinreichender Annäherung kann so der w-Wert für die Messung bestimmtwerden. Es ist allerdings darauf zu achten,dass die Daten in diesem Block einen Realitätsbezug haben; z.B. bei einer WAK > 30 Vol.-% erscheint die Frage: “Ist der Wert für WAK realistisch?“. Der aus dem Diagramm ermittelte w-Wert wird in die Tabelle (4. Block) „Ergebnisse“ eingetragen. Es erscheint außer dem eingegebenen WAK und dem daraus ermittelten w-Wert auch das aus diesen beiden Angaben errechnete Ergebnis für den Wassereindringkoeffizienten (B-Wert).
Die obige Auswertemaske entstammt der gleichnamigen Excel-Datei, “karsten2010-03“
Mathematische Erläuterungen zur Auswertung der Messdaten[Bearbeiten]
In dem Diagramm des obigen Auswerteschemas ist der w-Wert (w) eine Funktion des zeitabhängig kapillar aufgenommenen Wassers; diese Wassermenge (V) wird in Milliliter am Röhrchen abgelesen.
Für eine hinreichend genau an die Messwertkurve genäherte Funktion sind die Parameter bekannt - und damit auch für die Messwertkurve.
Im Prinzip wird im Auswerteschema versucht durch variieren der Wasseraufnahmekapazität (WAK) in einem vernünftigen Bereich die kapillar aufgenommene Wassermenge der zu berechnenden Funktion denen der Messwertkurve anzugleichen.
Diese berechnete aufgenommene Wassermenge (Vkar) hängt von der Saugfläche (A) des Karsten`schen Prüfröhrchens, von der Zeit (t) der Wasseraufnahme ab, sowie von den beiden Materialkonstanten, dem w-Wert (w) und der Wasseraufnahmekapazität (WAK) des zu untersuchenden Materials.
[Die Wasseraufnahmekapazität kann maximal gleich der Porosität werden; in der Regel sind sie etwas niedriger, da das kapillar aufgenommene Wasser nicht sofort den gesamten Porenraum ausfüllt.]
In den folgenden Abschnitten wird für die Messmethode zur Wasseraufnahme mit dem Karsten`schen Prüfröhrchen unter idealen Bedingungen die Volumen/Zeit-Funktion [V=f(t)] hergeleitet.
Kapillare Wasseraufnahme[Bearbeiten]
Im Labor werden üblicherweise die Wasseraufnahmekoeffizienten (w-Werte) von Baustoffen durch kapillare Wasseraufnahme an Bohrkernen oder Prismen bestimmt. Die Wasseraufnahme erfolgt über einen Saugvorgang in eindimensionaler Richtung. Dabei ist in erster Näherung die aufgenommene Wassermenge (m) proportional der Wurzel aus der Zeit (t).und ist von der Größe der Saugfläche (A) abhängig. Es gilt folgende Gleichung:
Gl.(1): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w=\frac{m}{A\cdot\sqrt{t}}\\}
w wird als Wasseraufnahmekoeffizient (w-Wert) bezeichnet und in kg/m2/h0,5 angegeben.
Ebenso kann ein Wassereindringkoeffizient (B-Wert) definiert werden. Dabei gilt näherungsweise, dass die Wassereindringtiefe (x) proportional der Wurzel aus der Zeit (t) ist.
Gl.(2): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B=\frac{x}{\sqrt{t}}\\}
Aus dem w- und B-Wert wird die Wasseraufnahmekapazität (WAK) unter Berücksichtigung von
Gl.(3) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta=\frac{m}{V}\\}
wie folgt hergeleitet:
Gl.(4): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle WAK=\frac{w}{B\cdot\delta}\\}
δ : Dichte des Wassers = 0,998 g/cm³ bei 20 °C ≈ 1 g/cm³
Die Wasseraufnahmekapazität (WAK) wird häufig auch in Volumenprozent angegeben:
Gl.(5) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle WAK\left[Vol.\%\right]=WAK\cdot 100\\}
Durch einsetzen von Gleichung 2 in Gleichung 4 ergibt sich für die Eindringtiefe (x):
Gl.(6) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=\frac{w\cdot\sqrt{t}}{WAK\cdot \delta}\\}
Wasseraufnahme nach Karsten[Bearbeiten]
Die Wasseraufnahme mittels dem Karsten`schen Prüfröhrchen stellt einen dreidimensionalen Saugvorgang dar; die Sauggeschwindigkeit ist in alle drei Richtungen gleich. Auch hier ist die Wassereindringtiefe proportional zur Wurzel aus der Zeit. Für die zeitabhängig kapillar aufgenommene Wassermenge gilt allerdings ein anderer - etwas komplizierter - mathematischer Zusammenhang. Dieser wird wie folgt abgeleitet.
Im Idealfall besitzt der Durchfeuchtungskörper die Form eines zentralen Zylinders, der von einem Vierteltorus umgeben ist. Die Grundfläche des Zylinders entspricht der des Karsten`schen Prüfröhrchens.
Gl.(7): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Zylinder}=\pi\cdot r^2\cdot x\\}
x = Höhe des Zylinders; (entspricht in dieser Berechnung der Wassereindringtiefe)
r = Radius des Zylinders; (entspricht dem Radius des Karsten´schen Prüfröhrchens)
3.2.1.) Guldinsche Regel:
Das Volumen des Vierteltorus lässt sich mit der Guldinschen Regel berechnen. Diese besagt:
Das Volumen eines Drehkörpers ist gleich dem Produkt aus dem Flächeninhalt der den Drehkörper erzeugende Fläche und der Länge des Weges, den der Schwerpunkt dieser Fläche bei einer Volldrehung um die Drehachse beschreibt.
Berechnung des Vierteltorus[Bearbeiten]
Um nun das Volumen des Vierteltorus nach dieser Regel berechnen zu können, benötigt man den Abstand zwischen der Drehachse und dem Schwerpunkt des Viertelkreises. Dieser Viertelkreis erzeugt durch eine Volldrehung seines Schwerpunktes um die Drehachse einen Vierteltorus. Genauso kann ein Halbkreis einen Vierteltorus erzeugen, wenn der sich ergebene Drehkörper senkrecht zur Drehachse halbiert wird.
Betrachtet man nun einen Halbkreis, dessen gerade Kante die Drehachse darstellt, so erhält man als Drehkörper eine Kugel.
Gl.(8): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Kugel}=\frac{4\cdot\pi \cdot x^3}{3}\\}
x = Radius der Kugel; (entspricht in dieser Berechnung der Wassereindringtiefe)
Mittels der Guldinschen Regel wird nun der Abstand (a) von der Drehachse bis zum Schwerpunkt des Halbkreises berechnet.
Gl.(9): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{4\cdot\pi \cdot x^3}{3}=\left(\frac{\pi\cdot x^2}{2}\right)\cdot (2\cdot\pi\cdot a)\\}
VKugel = (Fläche des Halbkreises) . (Weg des Schwerpunktes um die Drehachse)
Auflösen nach a:
Gl.(10): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a=\frac{4\cdot x}{3\cdot \pi}\\}
a = Entfernung des Schwerpunktes von der Drehachse
Der Schwerpunkt des Halbkreises ist von dessen Entfernung zur Drehachse unabhängig.
Wird diese Entfernung (a) um den Radius (r) des Karsten´schen Prüfröhrchens verlängert und der sich ausbildende Drehkörper senkrecht zur Drehachse halbiert, so erhält man das Volumen des Vierteltorus. a wird wie laut Gleichung 10 ersetzt.
Gl.(11) Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle _{VT}=\frac{\left(\frac{\pi\cdot x^2}{2}\right)\cdot (2\cdot\pi\cdot (r+a))}{2}=\frac{\pi^2\cdot r \cdot x^2}{2}+\frac{2\cdot \pi \cdot x^3}{3}\\}
VVT = Volumen des Vierteltorus
Berechnung des Durchdringungskörper[Bearbeiten]
Wird jetzt zum Volumen des Vierteltorus(Gl.10) noch das Volumen des zentralen Zylinders (Gl.7) addiert, erhält man das gesamte Durchfeuchtungsvolumen (VDkar), welches sich bei der Wasseraufnahme mit dem Karsten`schen Prüfröhrchen ausbildet:
Gl.(12): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Dkar}=\pi \cdot r^2 \cdot x + \frac{\pi^2\cdot r \cdot x^2}{2}+\frac{2\cdot \pi \cdot x^3}{3}\\}
3.3.) Berechnung des zeitabhängig kapillar aufgenommenen Wassers bei der Messmethode mit dem Karsten`schen Prüfröhrchen:
Die Wasseraufnahme wie auch die Wasseraufnahmekapazität eines Gesteins ist unabhängig von dessen Gewicht und dessen Volumen und somit auch von seiner Form. Dies bedeutet, dass das Verhältnis der Volumina der jeweils aufgenommenen Wassermenge zu deren Durchfeuchtungsvolumina in einem Körper bzw. einem Stein immer konstant bleibt. Daraus folgt:
Gl.(13): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{V_{kap}}{V_{Dkap}}=\frac{V_{kar}}{V_{Dkar}}\\}
Vkap : Aufgenommenes Wasservolumen bei kapillarer Wasseraufnahme mit eindimensionaler Saugrichtung
VDkap : Durchfeuchtungsvolumen bei kapillarer Wasseraufnahme mit eindimensionaler Saugrichtung
Vkar : Aufgenommenes Wasservolumen bei Wasseraufnahme nach Karsten (dreidimensionale Saugrichtung)
VDkar : Durchfeuchtungsvolumen bei Wasseraufnahme nach Karsten (dreidimensionale Saugrichtung)
Berechnung von Vkap[Bearbeiten]
Gl.(14): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w=\frac{m}{A\cdot\sqrt{t}}=\frac{V_{kap}\cdot\delta}{A\cdot\sqrt{t}}\\}
Gl.(15): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{kap}=\frac{w\cdot A \cdot \sqrt{t}}{\delta}\\}
Berechnung von VDkap[Bearbeiten]
Gl.(16): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Dkap}=A\cdot x\\}
A = Grundfläche des Karsten`schen Prüfröhrchens (zentraler Zylinder)
x = Wassereindringtiefe
Durch einsetzen des Terms für die Eindringtiefe (x) aus Gleichung 6 in Gleichung 16 erhält man:
Gl.(17): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Dkap}=\frac{A\cdot w\cdot\sqrt{t}}{WAK\cdot\delta}\\}
Aus Gleichung 13, 15 und 17 folgt
Gl.(18): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{V_{kap}}{V_{Dkap}}=\frac{V_{kar}}{V_{Dkar}}=\frac{WAK\cdot\delta\cdot w\cdot A\cdot\sqrt{t}}{\delta\cdot w\cdot A\cdot\sqrt{t}}=WAK\\}
Danach berechnet sich anhand der Gleichungen 12 und 18 die aufgenommene Wassermenge (Vkar) bei der Messung mit dem Karsten`schen Prüfröhrchen wie folgt
Gl.(19): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{kar}=WAK\cdot \pi\cdot r^2\cdot x+\frac{WAK\cdot\pi^2\cdot r\cdot x^2}{2}+\frac{2\cdot WAK\cdot \pi\cdot x^3}{3}\\}
Bei der Auswertung wird nicht der Radius (r) des Karsten`schen Röhrchens angegeben, sondern der Durchmesser (s.a. Gleichung 20)
Durch Einsetzen des in Gleichung 6 für die Eindringtiefe (x) ermittelten Terms wird die endgültige Funktion [V=f(t)] für die mit dem Karsten`schen Prüfröhrchen ideal kapillar aufgenommene Wassermenge erhalten:
Gl.(20): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{kar}=\frac{\pi\cdot d^2\cdot w\cdot\sqrt{t}}{4\cdot \delta}+\frac{\pi^2\cdot d\cdot w^2\cdot t}{4\cdot WAK\cdot \delta^2}+\frac{2\cdot\pi\cdot w^3\cdot t\cdot\sqrt{t}}{3\cdot WAK^2\cdot \delta^3}\\}
Werden die entsprechenden Parameter in diese Formel wie folgt eingetragen:
d [cm] ; w [kg/m2/h0,5] ; t [min]; δ = 1g/cm3 und WAK [Vol.%] so wird V[ml] erhalten:.
Gl.(21): Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \boxed{V_{kar}=0,01014\cdot d^2 \cdot w\cdot\sqrt{t}+\frac{0,0411\cdot d\cdot w^2\cdot t}{WAK} + \frac{0,045\cdot w^3\cdot t\cdot\sqrt{t}}{WAK^2}}}
Weblinks[Bearbeiten]
- ↑ http://www.baufachinformation.de/buch/234648 http://www.baufachinformation.de/buch/234648]; letzter Zugriff am 8.5.2013
Literatur[Bearbeiten]
Es wurden keine Zitate im Artikel gefunden.
· D´ham, Gerhard; Meinhardt, Jeannine; Niemeyer, Rolf (2010): Bestimmung der kapillaren Wasseraufnahme mit Messröhrchen nach Karsten und Mirowski. In: Auras, Michael; Meinhardt, Jeannine; Snethlage, Rolf (Hrsg.): Leitfaden Naturstein-Monitoring; IRB-Verlag, Stuttgart 2011 , S. 82 – 92.
· Bartsch, Hans-Jochen; Taschenbuch Mathematischer Formeln; VEB Fachbuchverlag Leipzig, Lizenzausgabe für den Verlag Harri Deutsch ∙ Thun; 4.Auflage; 1978; S.145.